What is RMS value? Easiest Explanation

• June 10, 2020
• Gaurav J

How many times we used the term RMS while dealing with AC circuits. Well, counting that is madness. Because, we use it almost every day. The voltage we receive in our home is a RMS value. The system voltages like 415V AC, 11kV AC, 36kV AC, etc are also RMS values. The RMS value is an important term in electrical engineering. But, what is the exact meaning of RMS value? And why it is so much important?

---

The use of RMS value is almost everywhere in electrical engineering. Therefore, every electrical engineer must know about RMS value. By the end of this tutorial you will be able to understand what is the exact meaning of RMS value and you will also be able to explain the meaning of RMS value to your teachers, friends, colleagues, etc. So, let’s get started.

Power Calculation; easy in DC, tough is AC!

We know that, voltage or current in case of DC systems, never changes its direction. At every instance, it almost remains constant. And hence calculating power, voltage or current is very easy in DC systems. Consider the example shown. Let’s say, a bulb is connected to a 10V DC source.

And the current flowing through the circuit is 2A. From this, we can easily calculate the power drawn by the bulb by simply multiplying the voltage with current, as both voltage and current are constant.

P =VI = 10 X 2 = 20W

And this is the power taken by the bulb at any instance. Now, if we change the DC source with AC. The voltage and current are no more constant. The value of voltage and current will now change continuously. For easy understanding, we will only consider the voltage waveform. In the beginning, Voltage will be zero after some time it will reach to 5 V, after some time it will go to 10V. Again after some time it will reduce to 5V, 0V, -5V, -10V, -5V, 0V and the cycle will continue.

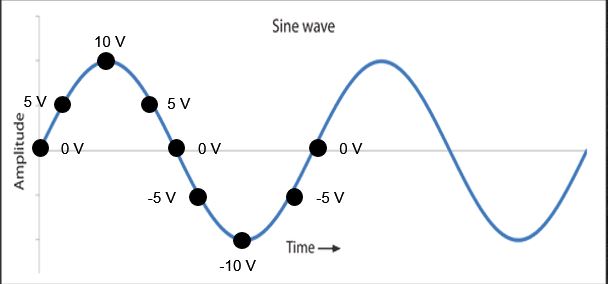
And if we considering either 5V to -5V or 10V to -10V which is the peak to peak value or any other value of voltage on the waveform for power calculation, it will lead to the wrong answer. Because, the value is only true for some particular time, after that time the value is different.

Things gets worse when we compare to different waveforms. For instance, if we are comparing sine wave with square wave, the sine wave will have its peak value for small amount of time than the square wave.

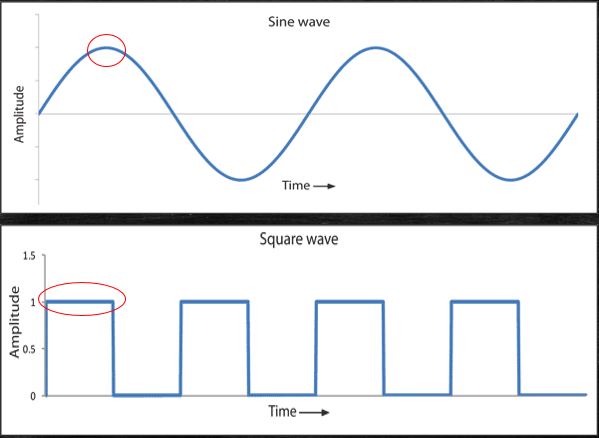
And hence the effect of these two AC voltages powering same load, would be different. In conclusion, considering the peak to peak value for calculations is not a good idea.

So, we need a solution for this. We need a term, which will give us the effective value of AC quantities. We need a term, which we can consider for power calculation and which will remain true for most of the time.

---

Effective Value of AC; Root Mean Square

Fortunately, we don’t have to worry, there is method to calculate the effective value in AC circuits. And how do we do it?

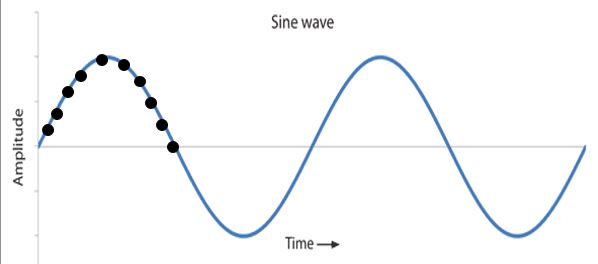
Step 1 – Divide the waveform in equal section.

Simply, mark the points on equal distance as shown. To understand we’ll consider only half cycle. If you want, you can also do it for second half cycle. The marked values are shown shown.

Step 2 – Take square of each value.

Simply take the “square”of each value you marked.

Step 3 – Take the Mean/average.

Now, calculate the “Mean” or average of the values.

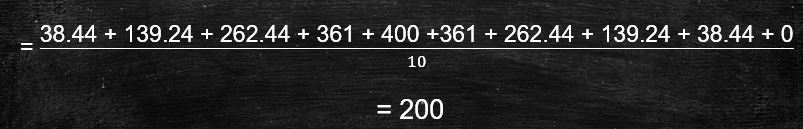
Step 4 – Square root.

And finally, take the square “root”of the final value.

The value we get from this method is known as “RMS value” i.e. Root Mean Square value.

So, in our example, the Peak value is 20 V (V5), where as, the effective value or the RMS value is 14.14 V. This 14.14 V AC is equal to the 14.14V DC. Which means, RMS value is equivalent to its DC value. To get the things more clearly, consider the example shown.

Here we have two different sources one is of 10 V AC RMS and other is 10 V DC. These sources are connected to the bulb who has resistance of 2 ohms. In case of DC circuit, power dissipated is 50 W. But, what about AC? As the 10 V is a RMS value, we can take it for the power calculation. As a result, power dissipated by AC circuit will also be 50 W.

---

RMS value is the best way to calculate the effective value of AC system. For instance, for calculating size of cable considering RMS current measurement is always helpful. But, for considering insulator in high voltage AC applications, Peak value shall be considered rather than RMS value.

RMS value, Peak value, Average value will change with different waveforms. These values will be different for sine wave, for square wave, for triangular wave, etc. To make things more easy, we also have a formula to calculate RMS value or peak value and it is given by –

V rms = 0.7071 x Vmax

Remember, this value is true only for pure form of “sine wave”.
So, we can also calculate the RMS value in our above example using the formula.

V rms = 0.7071 x 20 = 14.14 V

You can also find out, why AC supply is always represented by a Sine wave.

In conclusion, RMS value is an effective value of AC quantities which needs to be considered for different types of calculations and assumptions. RMS value is also equivalent to its DC value.